Ever since I started selling subscriptions for DocsAutomator, I've been fascinated by the likelihood of selling a certain number of subscriptions in a given day. It feels very random and not random at all — at the same time!
Intuitively, it's clear that if one subscription is sold on average per day, the likelihood of that event is not 1, but must be lower. Some days it's zero, another it's four. But how likely is selling one subscription then?
Welcome to the Poisson distribution. This distribution gives the probability of a number of events in a fixed time frame if the mean for that time frame is known. Only two numbers are needed for the result!
If I'm selling 30 subscriptions on average per month, so roughly one a day, the mean rate is 1. Since it's B2B, it more or less only applies to weekdays, so it's over 20 and not 30 days per month, turning the mean rate into 1.5 subscriptions per day.
With the help of this online calculator, we can now calculate the probability (λ = mean over time period, x = number of events)*:
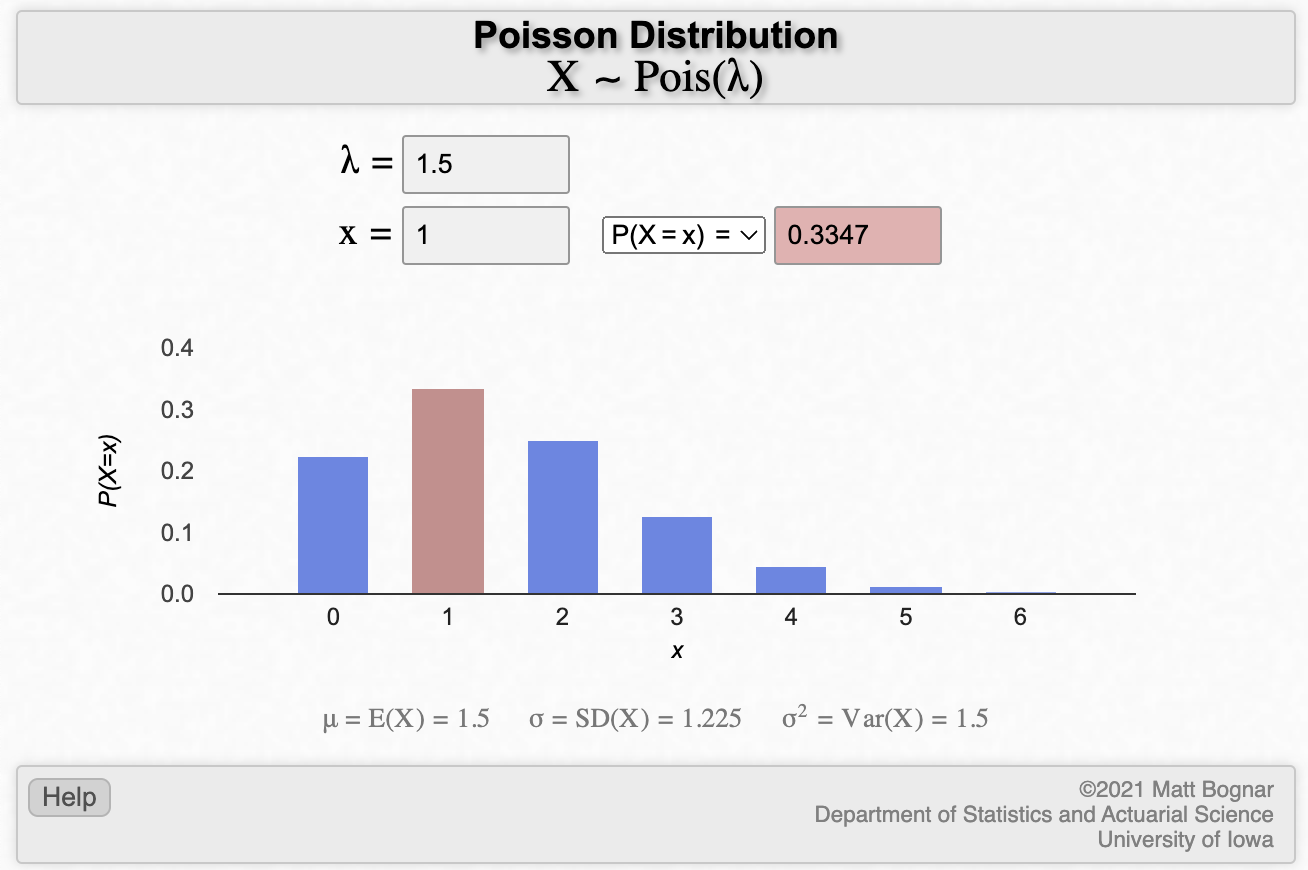
The likelihood of selling one subscription on a given day, when the average is 1,5 per day, is 33,4%! Probability for selling zero subscriptions is 22,3%. Selling five in a day? 1,4%! Selling zero two days in a row? 4,9%.
This is a reality check for my (often negativity-focused) intuition. Like many, I'm having much stronger emotions when there's little growth than when there's strong growth. If I sell zero subscriptions in a day, I feel like I'm going bankrupt and nothing's working anymore. If, however, I'm selling three subscriptions in a day, it feels good but also normal. This is how it's supposed to be. Comparing probabilities though, selling zero subscriptions is 10% more likely than selling three subscriptions (22% vs. 12%). This helps putting things in perspective.
So next time you're having a bad day due to slow growth: Maybe it's just a matter of probability!
*of course there are some simplifications by excluding seasonality, growth, etc.